Tutorials
This section demonstrates how to use DMDO to solve MDO problems.
Sellar problem
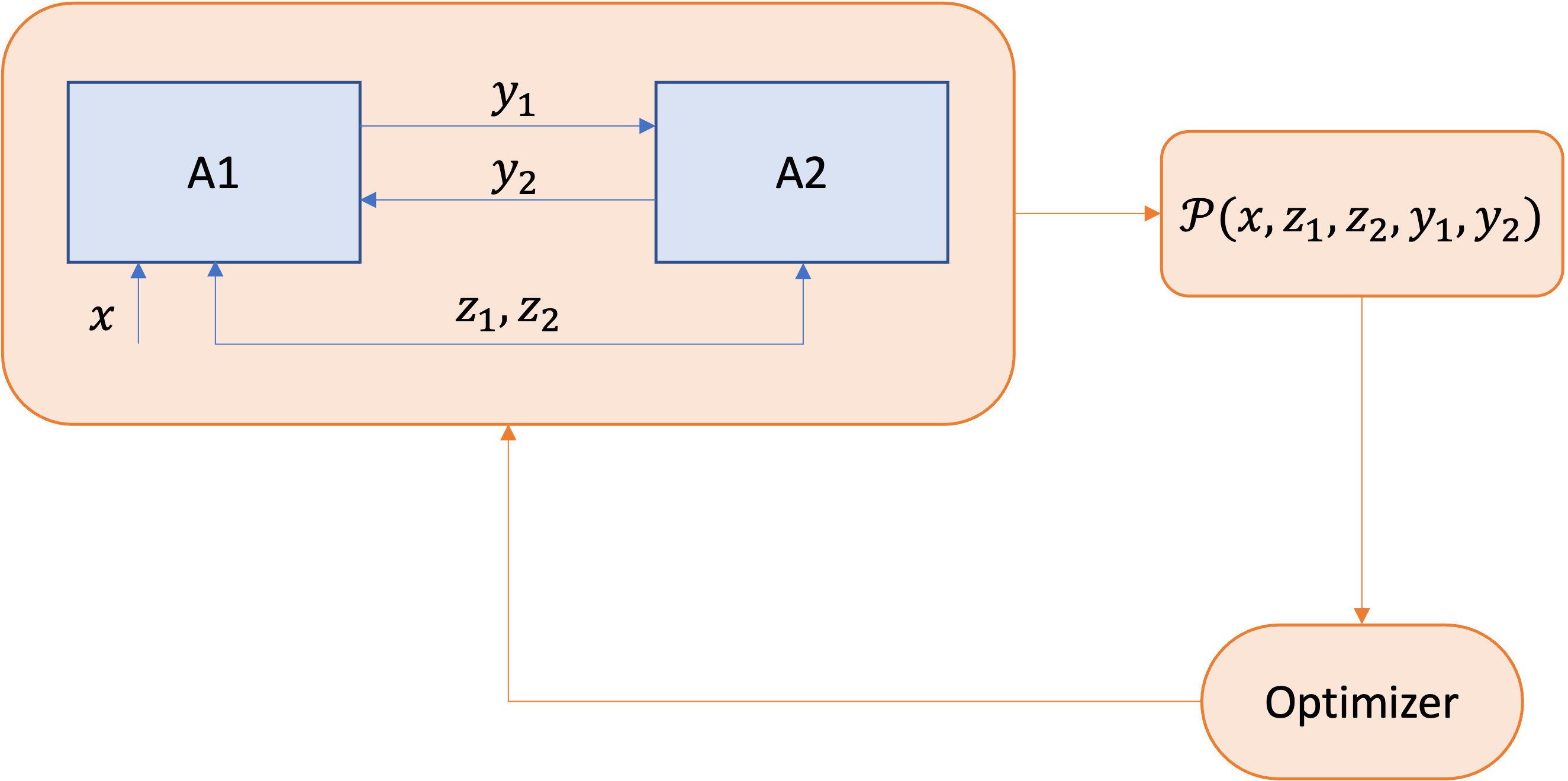
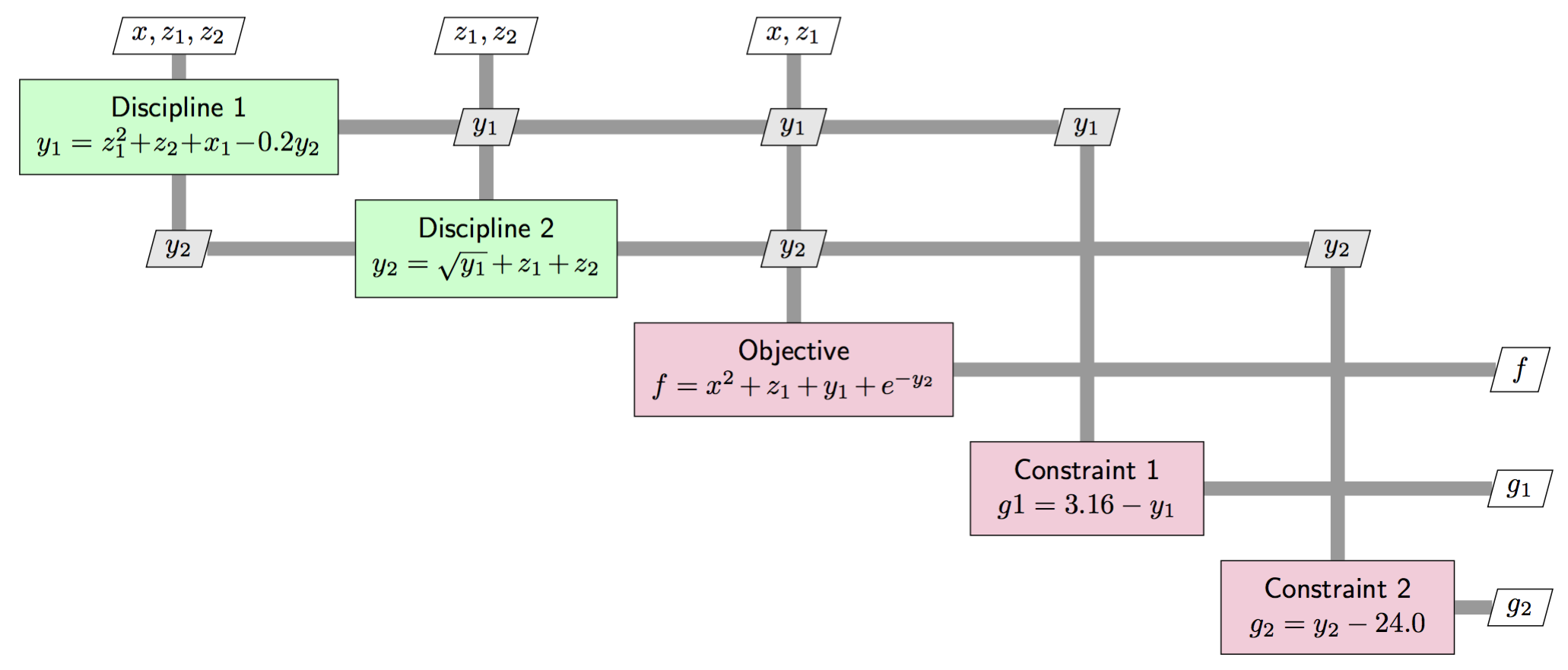
Original problem \(\mathcal{P}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ x^2 + z_2 + y_1 + e^{-y_2} \\
\text{w.r.t.}: & \ \ \ x, z_1, z_2 \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ 3.16 - y_1 <=0 \\
& \ \ \ y_2 - 24.0 <=0 \\
& \ \ \ y_1 (x, z_{1}, z_{2}, y_{2}) = x+z^{2}_{1}+z_{2}-0.2y_{2} \\
& \ \ \ y_2 (z_{1}, z_{2}, y_{1}) = \sqrt{y_{1}}+z_{1}+z_{2}
\tag{$\mathcal{P}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{1}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ x^2 + z_2 + y_1 + e^{-y_2} + \phi_{z_{1}} (z_{1_{1}}-z_{1_{2}}) + \phi_{z_{2}} (z_{2_{1}}-z_{2_{2}}) + \phi_{y_{1}} (y_{1_{1}}-y_{1_{2}}) + \phi_{y_{2}} (y_{2_{1}}-y_{2_{2}})\\
\text{w.r.t.}: & \ \ \ x, z_{1_{1}}, z_{2_{1}}, y_{2_{1}} \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ 3.16 - y_{1_{1}} <=0 \\
& \ \ \ y_{1_{1}} (x, z_{1_{1}}, z_{2_{1}}, y_{2_{1}}) = x+z^{2}_{1_{1}}+z_{2_{1}}-0.2y_{2_{1}}
\tag{$\mathcal{p}_{1}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{2}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ \phi_{z_{1}} (z_{1_{1}}-z_{1_{2}}) + \phi_{z_{2}} (z_{2_{1}}-z_{2_{2}}) + \phi_{y_{1}} (y_{1_{1}}-y_{1_{2}}) + \phi_{y_{2}} (y_{2_{1}}-y_{2_{2}}) \\
\text{w.r.t.}: & \ \ \ x, z_{1_{2}}, z_{2_{2}}, y_{1_{2}} \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ y_{2_{2}} - 24.0 <=0 \\
& \ \ \ y_{2_{2}} (z_{1_{2}}, z_{2_{2}}, y_{1_{2}}) = \sqrt{y_{1_{2}}}+z_{1_{2}}+z_{2_{2}}
\tag{$\mathcal{p}_{2}$}
\end{align*}\end{split}\]
# Sellar - Two discipline problem with IDF
# Variables grouping and problem setup
x = {}
X: List[variableData] = []
# Define variable names
N = ["x", "z1", "z2", "y1", "y2", "z1", "z2", "y1", "y2"]
nx: int = len(N)
# Subproblem indices: Indices should be non-zero
J = [1,1,1,1,1,2,2,2,2]
# Subproblems links
L = [None, 2, 2, 2, 2, 1, 1, 1, 1]
# Coupling types
Ct = [COUPLING_TYPE.UNCOUPLED,
COUPLING_TYPE.SHARED,
COUPLING_TYPE.SHARED,
COUPLING_TYPE.FEEDFORWARD,
COUPLING_TYPE.FEEDBACK,
COUPLING_TYPE.SHARED,
COUPLING_TYPE.SHARED,
COUPLING_TYPE.FEEDBACK,
COUPLING_TYPE.FEEDFORWARD]
# Realistic lower bounds
lb = [0, -10, 0, 3.16, 1.77763888346, -10, 0, 3.16, 1.77763888346]
# Realistic upper bounds
ub = [10.,10.,10., 115.2, 24., 10.,10., 115.2, 24.]
# # Artificial lower bounds
# lb = [0, -10, 0, 2., 1.5, -10, 0, 2., 1.5]
# # Artificial upper bounds
# ub = [10.,10.,10., 50., 50, 10.,10., 50., 50]
# Bad artificial lower bounds
# lb = [0, -10, 0, 0., 0., -10, 0, 0., 0.]
# Bad artificial upper bounds
# ub = [10.]*9
# Baseline
x0 = [0., 5., 5., 8.43, 7.848, 5., 5., 8.43, 7.848]
# Scaling
scaling = np.subtract(ub,lb)
Qscaling = []
# Create a dictionary for each variable
for i in range(nx):
x[f"var{i+1}"] = {"index": i+1,
"sp_index": J[i],
f"name": N[i],
"dim": 1,
"value": 0.,
"coupling_type": Ct[i],
"link": L[i],
"baseline": x0[i],
"scaling": scaling[i],
"lb": lb[i],
"value": x0[i],
"ub": ub[i]}
Qscaling.append(10./scaling[i] if 10./scaling[i] != np.inf and 10./scaling[i] != np.nan else 1.)
# Instantiate the variableData class for each variable using its according dictionary
for i in range(nx):
X.append(variableData(**x[f"var{i+1}"]))
def Sellar_A1(x):
return x[0] + x[1]**2 + x[2] - 0.2*x[3]
def Sellar_A2(x):
return x[0] + x[1] + np.sqrt(x[2])
def Sellar_opt1(x, y):
return [x[0]**2 + x[2] + y[0] + np.exp(-x[3]), [3.16-y[0]]]
def Sellar_opt2(x, y):
return [0., [y[0]-24.]]
# Analyses setup; construct disciplinary analyses
DA1: process = DA(inputs=[X[0], X[1], X[2], X[4]],
outputs=[X[3]],
blackbox=Sellar_A1,
links=2,
coupling_type=COUPLING_TYPE.FEEDFORWARD
)
DA2: process = DA(inputs=[X[5], X[6], X[7]],
outputs=[X[8]],
blackbox=Sellar_A2,
links=1,
coupling_type=COUPLING_TYPE.FEEDFORWARD
)
sp1_MDA: process = MDA(nAnalyses=1, analyses = [DA1], variables=[X[0], X[1], X[2], X[4]], responses=[X[3]])
sp2_MDA: process = MDA(nAnalyses=1, analyses = [DA2], variables=[X[5], X[6], X[7]], responses=[X[8]])
# Construct the coordinator
coord = ADMM(beta = 1.3,
nsp=2,
budget = 500,
index_of_master_SP=1,
display = True,
scaling = Qscaling,
mode = "serial",
M_update_scheme= w_scheme.MAX,
store_q_io=True
)
# Construct subproblems
sp1 = SubProblem(nv = 4,
index = 1,
vars = [X[0], X[1], X[2], X[4]],
resps = [X[3]],
is_main=1,
analysis= sp1_MDA,
coordination=coord,
opt=Sellar_opt1,
fmin_nop=np.inf,
budget=10,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST,
freal=3.16)
sp2 = SubProblem(nv = 3,
index = 2,
vars = [X[5], X[6], X[7]],
resps = [X[8]],
is_main=0,
analysis= sp2_MDA,
coordination=coord,
opt=Sellar_opt2,
fmin_nop=np.inf,
budget=10,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST
)
MDAO: MDO = MDO(
Architecture = MDO_ARCHITECTURE.IDF,
Coordinator = coord,
subProblems = [sp1, sp2],
variables = X,
responses = [X[3], X[8]],
fmin = np.inf,
hmin = np.inf,
display = False,
inc_stop = 1E-9,
stop = "Iteration budget exhausted",
tab_inc = [],
noprogress_stop = 1000
)
# Run the MDO problem
out = MDAO.run()
# Print summary output
print(f'------Run_Summary------')
print(MDAO.stop)
print(f'q = {MDAO.Coordinator.q}')
for i in MDAO.Coordinator.master_vars:
print(f'{i.name}_{i.sp_index} = {i.value}')
fmin = 0
hmax = -np.inf
for j in range(len(MDAO.subProblems)):
print(f'SP_{MDAO.subProblems[j].index}: fmin= {MDAO.subProblems[j].MDA_process.getOutputs()}, hmin= {MDAO.subProblems[j].opt([s.value for s in MDAO.subProblems[j].get_design_vars()] , MDAO.subProblems[j].MDA_process.getOutputs())[1]}')
fmin += sum(MDAO.subProblems[j].MDA_process.getOutputs())
hmin= MDAO.subProblems[j].opt([s.value for s in MDAO.subProblems[j].get_design_vars()] , MDAO.subProblems[j].MDA_process.getOutputs())[1]
if max(hmin) > hmax:
hmax = max(hmin)
print(f'P_main: fmin= {fmin}, hmax= {hmax}')
print(f'Final obj value of the main problem: \n {fmin}')
------Run_Summary------
Iteration budget exhausted
q = [ 2.34375000e-02 1.17187500e-02 -1.99577179e-09 -2.96638243e-02]
x_1 = 0.0
z1_1 = 1.375
z2_1 = 2.34375
y1_1 = 3.159999977639373
y2_1 = 5.371875111803135
z1_2 = 1.328125
z2_2 = 2.33203125
y1_2 = 3.16
y2_2 = 5.437795133463117
SP_1: fmin= [3.159999977639373], hmin= [2.2360627127682164e-08]
SP_2: fmin= [5.437795133463117], hmin= [-18.56220486653688]
P_main: fmin= 8.59779511110249, hmax= 2.2360627127682164e-08
Final obj value of the main problem:
8.59779511110249
Speed reducer
Original problem \(\mathcal{P}\):
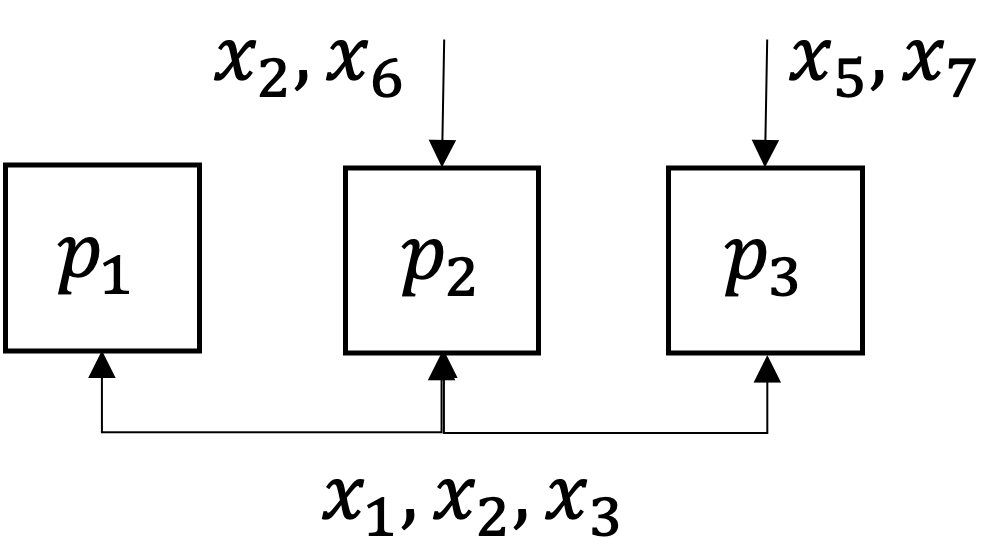
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ 0.7854x_{1}x^{2}_{2}(3.3333x^{2}_{3} + 14.9334x_{3} -43.0934) -1.5079x_{1}(x^{2}_{6} + x^{2}_{7}) +7.477(x^{3}_{6}+x^{3}_{7}) + 0.7854(x_{4}x^{2}_{6}+x_{5}x^{2}_{7}) \\
\text{w.r.t.}: & \ \ \ x_{1}, x_{2}, x_{3}, x_4, x_5, x_6, x_7 \\
\text{s.t. }: \ \ \ \\
& \ \ \ 27x^{-1}_{1}x^{-2}_{2}x^{-1}_{3} \leq 1 \\
& \ \ \ 397.5x^{-1}_{1}x^{-2}_{2}x^{-2}_{3} \leq 1 \\
& \ \ \ 1.93x^{-1}_{2}x^{-1}_{3}x^{3}_{4}x^{-4}_{6} \leq 1 \\
& \ \ \ 1.93x^{-1}_{2}x^{-1}_{3}x^{3}_{5}x^{-4}_{7} \leq 1 \\
& \ \ \ [(745x_{4}x^{-1}_{2}x^{-1}_{3})^{2} + 16.9 \times 10^{6}]^{0.5} / [ 110.0x^{3}_{6} ] \leq 1 \\
& \ \ \ [(745x_{5}x^{-1}_{2}x^{-1}_{3})^{2} + 157.5 \times 10^{6}]^{0.5} / [ 85.0x^{3}_{7} ] \leq 1 \\
& \ \ \ x_{2}x_{3}/40 \leq 1 \\
& \ \ \ 5x_{2}/x_1 \leq 1 \\
& \ \ \ x_{1}/12x_2 \leq 1 \\
& \ \ \ (1.5x_6 + 1.9)x^{-1}_4 \leq 1 \\
& \ \ \ (1.1x_7 + 1.9)x^{-1}_5 \leq 1 \\
& \ \ \ 2.6 \leq x_1 \leq 3.6\\
& \ \ \ 0.7 \leq x_2 \leq 0.8\\
& \ \ \ 17 \leq x_3 \leq 28\\
& \ \ \ 7.3 \leq x_4 \leq 8.3\\
& \ \ \ 7.3 \leq x_5 \leq 8.3\\
& \ \ \ 2.9 \leq x_6 \leq 3.9\\
& \ \ \ 5.0 \leq x_7 \leq 5.5\\
\tag{$\mathcal{P}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{1}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ 0.7854x_{1_{1}}x^{2}_{2_{1}}(3.3333x^{2}_{3_{1}} + 14.9334x_{3_{1}} -43.0934) + \phi_{x_{1_{12}}} (x_{1_{1}}-x_{1_{2}}) + \phi_{x_{1_{13}}} (x_{1_{1}}-x_{1_{3}}) + \phi_{x_{2_{12}}} (x_{2_{1}}-x_{2_{2}}) + \phi_{x_{2_{13}}} (x_{2_{1}}-x_{2_{3}}) + \phi_{x_{3_{12}}} (x_{3_{1}}-x_{3_{2}}) + \phi_{x_{3_{13}}} (x_{3_{1}}-x_{3_{3}})\\
\text{w.r.t.}: & \ \ \ x_{1_{1}}, x_{2_{1}}, x_{3_{1}} \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ 27x^{-1}_{1_{1}}x^{-2}_{2_{1}}x^{-1}_{3_{1}} \leq 1 \\
& \ \ \ 397.5x^{-1}_{1_{1}}x^{-2}_{2_{1}}x^{-2}_{3_{1}} \leq 1 \\
& \ \ \ x_{2_{1}}x_{3_{1}}/40 \leq 1 \\
& \ \ \ 5x_{2_{1}}/x_{1_{1}} \leq 1 \\
& \ \ \ x_{1_{1}}/12x_{2_{1}} \leq 1 \\
\tag{$\mathcal{p}_{1}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{2}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ -1.5079x_{1_{2}}(x^{2}_{6} + x^{2}_{7}) +7.477(x^{3}_{6}+x^{3}_{7}) + \phi_{x_{1_{12}}} (x_{1_{1}}-x_{1_{2}}) + \phi_{x_{1_{13}}} (x_{1_{1}}-x_{1_{3}}) + \phi_{x_{2_{12}}} (x_{2_{1}}-x_{2_{2}}) + \phi_{x_{2_{13}}} (x_{2_{1}}-x_{2_{3}}) + \phi_{x_{3_{12}}} (x_{3_{1}}-x_{3_{2}}) + \phi_{x_{3_{13}}} (x_{3_{1}}-x_{3_{3}})\\
\text{w.r.t.}: & \ \ \ x_{1_{1}}, x_{2_{1}}, x_{3_{1}}, x_4, x_6 \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ 1.93x^{-1}_{2_{2}}x^{-1}_{3_{2}}x^{3}_{4_{2}}x^{-4}_{6} \leq 1 \\
& \ \ \ (1.5x_6 + 1.9)x^{-1}_{4_{2}} \leq 1 \\
& \ \ \ [(745x_{4}x^{-1}_{2_{2}}x^{-1}_{3_{2}})^{2} + 16.9 \times 10^{6}]^{0.5} / [ 110.0x^{3}_{6} ] \leq 1
\tag{$\mathcal{p}_{2}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{3}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ 0.7854(x_{4_{3}}x^{2}_{6}+x_{5}x^{2}_{7}) + \phi_{x_{1_{12}}} (x_{1_{1}}-x_{1_{2}}) + \phi_{x_{1_{13}}} (x_{1_{1}}-x_{1_{3}}) + \phi_{x_{2_{12}}} (x_{2_{1}}-x_{2_{2}}) + \phi_{x_{2_{13}}} (x_{2_{1}}-x_{2_{3}}) + \phi_{x_{3_{12}}} (x_{3_{1}}-x_{3_{2}}) + \phi_{x_{3_{13}}} (x_{3_{1}}-x_{3_{3}})\\
\text{w.r.t.}: & \ \ \ x_{1_{3}}, x_{2_{3}}, x_{3_{3}}, x_{5}, x_{7} \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ [(745x_{5}x^{-1}_{2_{3}}x^{-1}_{3_{3}})^{2} + 157.5 \times 10^{6}]^{0.5} / [ 85.0x^{3}_{7} ] \leq 1 \\
& \ \ \ (1.1x_7 + 1.9)x^{-1}_5 \leq 1 \\
& \ \ \ 1.93x^{-1}_{2_{3}}x^{-1}_{3_{3}}x^{3}_{5}x^{-4}_{7} \leq 1
\tag{$\mathcal{p}_{3}$}
\end{align*}\end{split}\]
def SR_A1(x):
""" Speed reducer A1 """
return (0.7854*x[0]*x[1]**2*(3.3333*x[2]*x[2] + 14.9335*x[2] - 43.0934))
def SR_A2(x):
""" Speed reducer A2 """
return (-1.5079*x[0]*x[4]**2) + (7.477 * x[4]**3)
def SR_A3(x):
""" Speed reducer A3 """
return 0.7854 * x[3] * x[4]**2
def SR_opt1(x, y):
g5 = 27/(x[0]*x[1]**2*x[2]) -1
g6 = 397.5/(x[0]*x[1]**2*x[2]**2) -1
g9 = x[1]*x[2]/40 -1
g10 = 5*x[1]/x[0] -1
g11 = x[0]/(12*x[1]) -1
return [y, [g5,g6,g9,g10,g11]]
def SR_opt2(x, y):
g1 = np.sqrt( ((745*x[3])/(x[1]*x[2]))**2 + 1.69e+7)/(110*x[4]**3) -1
g3 = (1.5*x[4] + 1.9)/x[3] -1
g7 = 1.93*x[3]**3/(x[1]*x[2]*x[4]**4) -1
return [y, [g1,g3,g7]]
def SR_opt3(x, y):
g2 = np.sqrt( ((745*x[3])/(x[1]*x[2]))**2 + 1.575e+8)/(85*x[4]**3) -1
g4 = (1.1*x[4] + 1.9)/x[3] -1
g8 = (1.93*x[3]**3)/(x[1]*x[2]*x[4]**4) -1
return [y, [g2, g4, g8]]
# Variables setup
f1min = 722
f1max = 5408
f2min = 184
f2max = 506
f3min = 942
f3max = 1369
#
v = {}
V: List[variableData] = []
s = COUPLING_TYPE.SHARED
ff = COUPLING_TYPE.FEEDFORWARD
fb = COUPLING_TYPE.FEEDBACK
un = COUPLING_TYPE.UNCOUPLED
dum = COUPLING_TYPE.DUMMY
names = ["x1", "x2", "x3", "f1", "x1", "x2", "x3", "x4", "x6", "f2", "x1", "x2", "x3", "x5", "x7", "f3"]
spi = [ 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3]
links = [[2,3],[2,3],[2,3], None, [1,3],[1,3],[1,3], None, None, None, [1,2],[1,2],[1,2], None, None, None]
lb = [2.6 , 0.7 , 17., 722., 2.6 , 0.7, 17., 7.3, 2.9, 184., 2.6 , 0.7, 17., 7.3, 5.,942.]
ub = [3.6 , 0.8 , 28.,5408., 3.6 , 0.8, 28., 8.3, 3.9, 506., 3.6 , 0.8 , 28., 8.3, 5.5,1369.]
bl = np.divide(np.subtract(ub, lb), 2.)
coupling_t = \
[ s, s, s, un, s, s, s, un, un, un, s, s, s, un, un, un]
scaling = [10.] * 16
# Variables dictionary with subproblems link
for i in range(16):
v[f"var{i+1}"] = {"index": i+1,
"sp_index": spi[i],
f"name": names[i],
"dim": 1,
"value": 0.,
"coupling_type": coupling_t[i],
"link": links[i],
"baseline": bl[i],
"scaling": scaling[i],
"lb": lb[i],
"value": bl[i],
"ub": ub[i]}
for i in range(16):
V.append(variableData(**v[f"var{i+1}"]))
# Analyses setup; construct disciplinary analyses
DA1: process = DA(inputs=[V[0], V[1], V[2]],
outputs=[V[3]],
blackbox=SR_A1,
links=[4],
coupling_type=COUPLING_TYPE.FEEDFORWARD)
DA2: process = DA(inputs=[V[4], V[5], V[6], V[7], V[8]],
outputs=[V[9]],
blackbox=SR_A2,
links=[4],
coupling_type=COUPLING_TYPE.FEEDFORWARD
)
DA3: process = DA(inputs=[V[10], V[11], V[12], V[13], V[14]],
outputs=[V[15]],
blackbox=SR_A3,
links=[4],
coupling_type=COUPLING_TYPE.FEEDFORWARD
)
# MDA setup; construct subproblems MDA
sp1_MDA: process = MDA(nAnalyses=1, analyses = [DA1], variables=[V[0], V[1], V[2]], responses=[V[3]])
sp2_MDA: process = MDA(nAnalyses=1, analyses = [DA2], variables=[V[4], V[5], V[6], V[7], V[8]], responses=[V[9]])
sp3_MDA: process = MDA(nAnalyses=1, analyses = [DA3], variables=[V[10], V[11], V[12], V[13], V[14]], responses=[V[15]])
# Construct the coordinator
coord = ADMM(beta = 1.3,
nsp=4,
budget = 50,
index_of_master_SP=1,
display = True,
scaling = 0.1,
mode = "serial",
M_update_scheme= w_scheme.MEDIAN
)
# Construct subproblems
sp1 = SubProblem(nv = 3,
index = 1,
vars = [V[0], V[1], V[2]],
resps = [V[3]],
is_main=1,
analysis= sp1_MDA,
coordination=coord,
opt=SR_opt1,
fmin_nop=np.inf,
budget=20,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST)
sp2 = SubProblem(nv = 5,
index = 2,
vars = [V[4], V[5], V[6], V[7], V[8]],
resps = [V[9]],
is_main=0,
analysis= sp2_MDA,
coordination=coord,
opt=SR_opt2,
fmin_nop=np.inf,
budget=20,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST
)
sp3 = SubProblem(nv = 5,
index = 3,
vars = [V[10], V[11], V[12], V[13], V[14]],
resps = [V[15]],
is_main=0,
analysis= sp3_MDA,
coordination=coord,
opt=SR_opt3,
fmin_nop=np.inf,
budget=20,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST)
# Construct MDO workflow
MDAO: MDO = MDO(
Architecture = MDO_ARCHITECTURE.IDF,
Coordinator = coord,
subProblems = [sp1, sp2, sp3],
variables = V,
responses = [V[3], V[9], V[15]],
fmin = np.inf,
hmin = np.inf,
display = False,
inc_stop = 1E-9,
stop = "Iteration budget exhausted",
tab_inc = [],
noprogress_stop = 100
)
# Run the MDO problem
out = MDAO.run()
print(f'------Run_Summary------')
print(MDAO.stop)
print(f'q = {MDAO.Coordinator.q}')
for i in MDAO.Coordinator.master_vars:
print(f'{i.name}_{i.sp_index} = {i.value}')
fmin = 0
hmax = -np.inf
for j in range(len(MDAO.subProblems)):
print(f'SP_{MDAO.subProblems[j].index}: fmin= {MDAO.subProblems[j].MDA_process.getOutputs()}, hmin= {MDAO.subProblems[j].opt([s.value for s in MDAO.subProblems[j].get_design_vars()] , [])[1]}')
fmin += sum(MDAO.subProblems[j].MDA_process.getOutputs())
hmin= MDAO.subProblems[j].opt([s.value for s in MDAO.subProblems[j].get_design_vars()] , [])[1]
if max(hmin) > hmax:
hmax = max(hmin)
print(f'P_main: fmin= {fmin}, hmax= {hmax}')
print(f'Final obj value of the main problem: \n {fmin}')
Stop: qmax = 5.822068604999231e-10 < 1e-09
------Run_Summary------
Max inconsitency is below stopping threshold
q = [-7.82041099e-14 -5.82206860e-10 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00]
x1_1 = 3.4999998893203155
x2_1 = 0.7
x3_1 = 17.0
f1_1 = 1581.466590697449
x1_2 = 3.4999998893210975
x2_2 = 0.7
x3_2 = 17.0
x4_2 = 7.3
x6_2 = 3.3502146307821015
f2_2 = 221.91863685660422
x1_3 = 3.499999895142384
x2_3 = 0.7
x3_3 = 17.0
x5_3 = 7.715319699048533
x7_3 = 5.286654424469452
f3_3 = 169.3583713823956
Geometric programming
Original problem \(\mathcal{P}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ z^{2}_1 + z^{2}_2 \\
\text{w.r.t.}: & \ \ \ z_{1}, z_{2}, z_{3}, z_4, z_5, z_6, z_7, z_8, z_9, z_{10}, z_{11}, z_{12}, z_{13}, z_{14} \\
\text{s.t. }: \ \ \ & z_{i} \in [10^{-6}, 10^6 ] \ \ \forall i \\
& \ \ \ z^{2}_1 = z^{2}_{3} + z^{-2}_{4} + z^{2}_{5} \\
& \ \ \ z^{2}_2 = z^{2}_{5} + z^{2}_{6} + z^{2}_{7} \\
& \ \ \ z^{2}_3 = z^{2}_{8} + z^{-2}_{9} + z^{-2}_{10} + z^{2}_{11}\\
& \ \ \ z^{2}_6 = z^{2}_{11} + z^{2}_{12} + z^{2}_{13} + z^{2}_{14} \\
& \ \ \ z^{-2}_3 + z^{2}_{4} - z^{2}_{5} \leq 0 \\
& \ \ \ z^{2}_5 + z^{-2}_{6} - z^{2}_{7} \leq 0 \\
& \ \ \ z^{2}_8 + z^{2}_{9} - z^{2}_{11} \leq 0 \\
& \ \ \ z^{-2}_8 + z^{2}_{10} - z^{2}_{11} \leq 0 \\
& \ \ \ z^{2}_{11} + z^{-2}_{12} - z^{2}_{13} \leq 0 \\
& \ \ \ z^{2}_{11} + z^{2}_{12} - z^{2}_{14} \leq 0
\tag{$\mathcal{P}$}
\end{align*}\end{split}\]
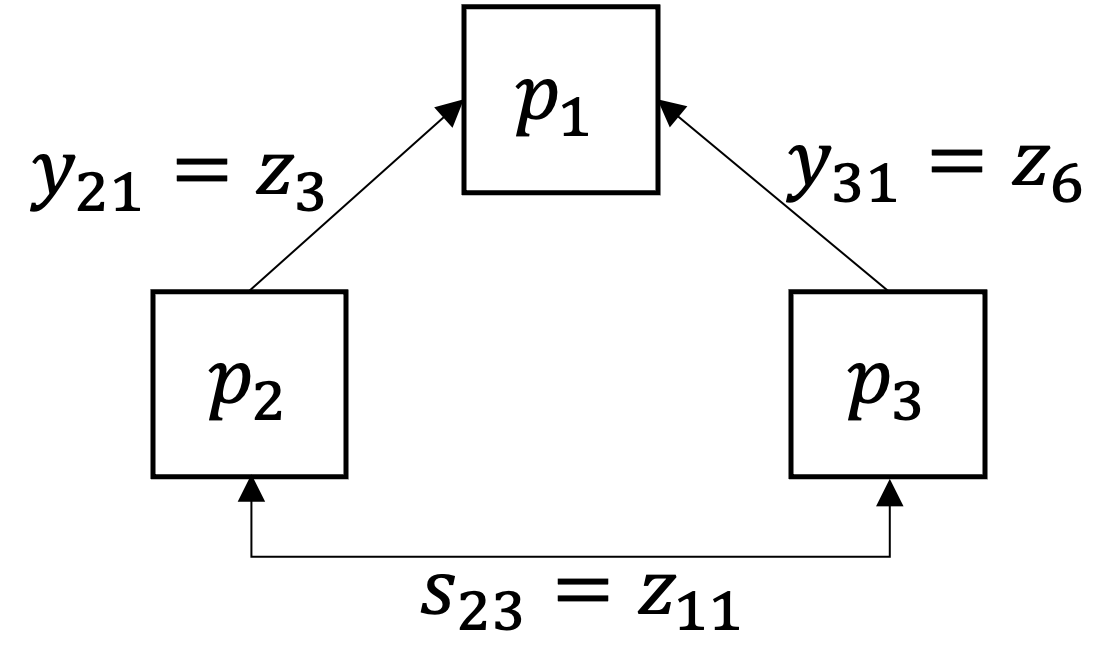
Subproblem \(\mathcal{p}_{1}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ t^{2}_{y_{21}} + t^{2}_{y_{31}} + z^{-2}_4 + 2z^{2}_{5}+ z^{2}_{7} + \phi_{y_{21}} (t_{y_{21}}-r_{y_{21}}) + \phi_{y_{31}} (t_{y_{31}}-r_{y_{31}})\\
\text{w.r.t.}: & \ \ \ t_{y_{21}}, t_{y_{31}}, z_{4}, z_{5}, z_{7} \in [10^{-6}; 10^{6}] \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ t^{-2}_{y_{21}}+z^{2}_{4}-z^{2}_{5} \leq 0 \\
& \ \ \ z^{2}_{5} + t^{-2}_{y_{31}} - z^{2}_{7} \leq 0
\tag{$\mathcal{p}_{1}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{2}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ \phi_{y_{21}} (t_{y_{21}}-r_{y_{21}}) + \phi_{s_{23}} (t_{s_{23}}-r_{s_{23}})\\
\text{w.r.t.}: & \ \ \ z_8, z_9, z_{10}, t_{s_{23}} \in [10^{-6}; 10^{6}] \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ z^{2}_8 + z^{2}_{9} - t^{2}_{s_{23}} \leq 0 \\
& \ \ \ z^{-2}_8 + z^{2}_{10} - t^{2}_{s_{23}} \leq 0 \\
\text{where} & \ \ \ r_{y_{21}} = \sqrt{z^{2}_{8}+z^{-2}_{9}+z^{-2}_{10}+t^{2}_{s_{23}}}
\tag{$\mathcal{p}_{2}$}
\end{align*}\end{split}\]
Subproblem \(\mathcal{p}_{3}\):
\[\begin{split}\begin{align*}
\text{min}: & \ \ \ \phi_{y_{31}} (t_{y_{31}}-r_{y_{31}}) + \phi_{s_{23}} (t_{s_{23}}-r_{s_{23}})\\
\text{w.r.t.}: & \ \ \ z_{12}, z_{13}, z_{14}, r_{s_{23}} \in [10^{-6}; 10^{6}] \\
\text{s.t. }: & \ \ \ & \\
& \ \ \ r^{2}_{s_{23}} + z^{-2}_{12} - z^{2}_{13} \leq 0 \\
& \ \ \ r^{2}_{s_{23}} + z^{2}_{12} - z^{2}_{14} \leq 0 \\
\text{where} & \ \ \ r_{y_{31}} = \sqrt{r^{2}_{s_{23}} + z^{2}_{12} +z^{2}_{13} + z^{2}_{14}}
\tag{$\mathcal{p}_{3}$}
\end{align*}\end{split}\]
def GP_A1(z):
z1 = np.sqrt(z[0]**2 + z[1]**-2 + z[2]**2)
z2 = np.sqrt(z[2]**2 + z[3]**2 + z[4]**2)
return z1**2 + z2**2
def GP_opt1(z,y):
if isinstance(y, list) and len(y) > 0:
return [y[0], [z[0]**-2 + z[1]**2 - z[2]**2, z[2]**2 + z[3]**-2 - z[4]**2]]
else:
return [y, [z[0]**-2 + z[1]**2 - z[2]**2, z[2]**2 + z[3]**-2 - z[4]**2]]
def GP_A2(z):
z3 = np.sqrt(z[0]**2 + z[1]**-2 + z[2]**-2 + z[3]**2)
return z3
def GP_opt2(z,y):
return [0, [z[0]**2 + z[1]**2 - z[3]**2, z[0]**-2 + z[2]**2 - z[3]**2]]
def GP_A3(z):
z6 = np.sqrt(z[0]**2 + z[1]**2 + z[2]**2 +z[3] **2)
return z6
def GP_opt3(z, y):
return [0, [z[0]**2 + z[1]**-2 - z[2]**2, z[0]**2 +z[1]**2 - z[3]**2]]
v = {}
V: List[variableData] = []
s = COUPLING_TYPE.SHARED
ff = COUPLING_TYPE.FEEDFORWARD
fb = COUPLING_TYPE.FEEDBACK
un = COUPLING_TYPE.UNCOUPLED
dum = COUPLING_TYPE.DUMMY
names = ["z3", "z4", "z5", "z6", "z7", "z3", "z8", "z9", "z10", "z11", "z6", "z11", "z12", "z13", "z14", "dd"]
spi = [ 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 1]
links = [ 2, None, None, 3, None, 1, None, None, None, 3, 1, 2, None, None, None, None]
coupling_t = \
[ fb, un, un, fb, un, ff, un, un, un, s, ff, s, un, un, un, ff]
lb = [1e-6]*15
ub = [1e6]*15
bl = [1.]*15
scaling = [9.e5] * 15
lb.append(15)
ub.append(18)
bl.append(GP_A1([1]*5))
scaling.append(1)
# Variables dictionary with subproblems link
for i in range(16):
v[f"var{i+1}"] = {"index": i+1,
"sp_index": spi[i],
f"name": names[i],
"dim": 1,
"coupling_type": coupling_t[i],
"link": links[i],
"baseline": bl[i],
"scaling": scaling[i],
"lb": lb[i],
"value": bl[i],
"ub": ub[i]}
for i in range(16):
V.append(variableData(**v[f"var{i+1}"]))
# Analyses setup; construct disciplinary analyses
DA1: process = DA(inputs=[V[0], V[1], V[2], V[3], V[4]],
outputs=[V[15]],
blackbox=GP_A1,
links=[2, 3],
coupling_type=COUPLING_TYPE.FEEDBACK)
DA2: process = DA(inputs=[V[6], V[7], V[8], V[9]],
outputs=[V[5]],
blackbox=GP_A2,
links=[1, 3],
coupling_type=COUPLING_TYPE.FEEDFORWARD
)
DA3: process = DA(inputs=[V[11], V[12], V[13], V[14]],
outputs=[V[10]],
blackbox=GP_A3,
links=[1, 2],
coupling_type=COUPLING_TYPE.FEEDFORWARD
)
# MDA setup; construct subproblems MDA
sp1_MDA: process = MDA(nAnalyses=1, analyses = [DA1], variables=[V[0], V[1], V[2], V[3], V[4]], responses=[V[15]])
sp2_MDA: process = MDA(nAnalyses=1, analyses = [DA2], variables=[V[6], V[7], V[8], V[9]], responses=[V[5]])
sp3_MDA: process = MDA(nAnalyses=1, analyses = [DA3], variables=[V[11], V[12], V[13], V[14]], responses=[V[10]])
# Construct the coordinator
coord = ADMM(beta = 1.3,
nsp=3,
budget = 200,
index_of_master_SP=1,
display = True,
scaling = 1.,
mode = "serial",
M_update_scheme= w_scheme.MEDIAN
)
# Construct subproblems
sp1 = SubProblem(nv = 5,
index = 1,
vars = [V[0], V[1], V[2], V[3], V[4]],
resps = [V[15]],
is_main=1,
analysis= sp1_MDA,
coordination=coord,
opt=GP_opt1,
fmin_nop=np.inf,
budget=5,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST,
freal=15.)
sp2 = SubProblem(nv = 4,
index = 2,
vars = [V[6], V[7], V[8], V[9]],
resps = [V[5]],
is_main=0,
analysis= sp2_MDA,
coordination=coord,
opt=GP_opt2,
fmin_nop=np.inf,
budget=20,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST
)
sp3 = SubProblem(nv = 4,
index = 3,
vars = [V[11], V[12], V[13], V[14]],
resps = [V[10]],
is_main=0,
analysis= sp3_MDA,
coordination=coord,
opt=GP_opt3,
fmin_nop=np.inf,
budget=20,
display=False,
psize = 1.,
pupdate=PSIZE_UPDATE.LAST)
# Construct MDO workflow
MDAO: MDO = MDO(
Architecture = MDO_ARCHITECTURE.IDF,
Coordinator = coord,
subProblems = [sp1, sp2, sp3],
variables = V,
responses = [V[5], V[10], V[15]],
fmin = np.inf,
hmin = np.inf,
display = False,
inc_stop = 1E-9,
stop = "Iteration budget exhausted",
tab_inc = [],
noprogress_stop = 100
)
# Run the MDO problem
out = MDAO.run()
print(f'------Run_Summary------')
print(MDAO.stop)
print(f'q = {MDAO.Coordinator.q}')
xsp2 = []
xsp3 = []
index = np.argmax(MDAO.Coordinator.q)
for i in MDAO.Coordinator.master_vars:
if i.sp_index == MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].link:
xsp2.append(i.value)
if i.sp_index == MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].link:
xsp3.append(i.value)
print(f'{i.name}_{i.sp_index} = {i.value}')
fmin = 0
hmax = -np.inf
for j in range(len(MDAO.subProblems)):
print(f'SP_{MDAO.subProblems[j].index}: fmin= {MDAO.subProblems[j].MDA_process.getOutputs()}, hmin= {MDAO.subProblems[j].opt([s.value for s in MDAO.subProblems[j].get_design_vars()] , [])[1]}')
if MDAO.subProblems[j].is_main:
fmin = MDAO.subProblems[j].MDA_process.getOutputs()
hmin= MDAO.subProblems[j].opt([s.value for s in MDAO.subProblems[j].get_design_vars()] , [])[1]
if max(hmin) > hmax:
hmax = max(hmin)
print(f'P_main: fmin= {fmin}, hmax= {hmax}')
print(f'Final obj value of the main problem: \n {fmin}')
# Checking the impact of swapping z11_2 and z11_3 on the feasibility of SP2 and SP3, respectively
temp = copy.deepcopy(xsp3[1])
xsp3[1] = xsp2[-1]
xsp2[-1] = temp
print(f'For {MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].name}_'
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].link} to '
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].name}_'
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].link}, using {MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].name}_'
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].link}'
f' will make h_sp{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].link} = {GP_opt2(xsp2, 0)[1]}')
print(f'For {MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].name}_'
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].link} to '
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].name}_'
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].link}, using {MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].name}_'
f'{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[1,index]-1].link}'
f' will make h_sp{MDAO.Coordinator.master_vars[MDAO.Coordinator._linker[0,index]-1].link} = {GP_opt3(xsp3, 0)[1]}')
------Run_Summary------
Iteration budget exhausted
q = [3.23003112e-07 1.43060452e-05 8.90277829e-01]
z3_1 = 2.398289998370998
z4_1 = 0.7582329644099639
z5_1 = 1.11111211111
z6_1 = 1.8764552402611754
z7_1 = 1.2323147798018002
z3_2 = 2.3982896753678857
z8_2 = 1.0481650186930753
z9_2 = 0.7709432938460119
z10_2 = 0.8846995034714752
z11_2 = 1.3011546553413305
z6_3 = 1.8764409342160242
z11_3 = 0.4108768262121927
z12_3 = 1.0071582788266598
z13_3 = 1.0745489499032588
z14_3 = 1.08774425713769
dd_1 = 14.99999996837727
SP_1: fmin= [14.99999996837727], hmin= [-0.4857941233010683, -2.6165797838650917e-05]
SP_2: fmin= [2.3982896753678857], hmin= [3.1621576690454845e-08, -0.00010216561395548496]
SP_3: fmin= [1.8764409342160242], hmin= [3.162211648088942e-08, -4.008740894789753e-09]
P_main: fmin= [14.99999996837727], hmax= -2.6165797838650917e-05
Final obj value of the main problem:
[14.99999996837727]
For z11_3 to z11_2, using z11_3 will make h_sp2 = [6.067750061945379, -0.014480830449391968]
For z11_3 to z11_2, using z11_2 will make h_sp3 = [3.097329036049318, 4.059378570979726]